Lesson 4

- Lesson 4 -
The string in the strings

String vibrations are at the very core of a large number of musical instruments used in a wide range of musical styles throughout the world. The basic math equation that governs vibration on strings is known as the wave equation. Different versions of this same basic equation describe wave phenomena of all types, including waves on the ocean to electromagnetic waves by which our televisions and radios transmit information, ultrasonic waves used to create images inside the body, and electromagnetic microwaves that we use to cook our food. It is the same equation used to describe vibrations of air in a tube, like those in brass and woodwind instruments. Click here to link to a mathematical derivation of the wave equation for string vibrations.

For the strings of musical instruments that are plucked or bowed, there are 3 primary things that determine at what frequencies that string will vibrate:

The length of the string: L ... which can be shortened on some instruments by the musician's fingers (violin family, guitar)
The mass per unit length of the string: µ
The tension of the string: T ... which is adjusted by musicians in order to "tune" their instrument

A string with a certain combination of L, T, and µ will tend to vibrate at certain frequencies, known as the resonant frequencies. These resonant frequencies for a string in air are nearly the same as the natural frequencies and are given by the following equation:

So there are actually an infinite number of natural frequencies f_n for a given string. Each of these natural frequencies is associated with a particular pattern of motion of the string, known as a mode of vibration or mode shape. Click here to review of derivation of the above equation from the fundamental law of physical motion discovered by Isaac Newton (college level math).

Click here for an animated-audio presentation of natural frequencies and associated vibration patterns for a string.

Now, which combination of these patterns (modes) and associated frequencies will occur depends on how and where the string is driven, by plucking or bowing it.

Plucked Strings
Plucked strings are essentially pulled sideways at a certain location and then let go. The shape of the string when it is let go will determine which modes of vibration and associated natural frequencies are excited. The modeshapes presented in the above demonstration can be combined together to create any initial deflection pattern of the string. What if the string was plucked at exactly it's middle location? See below.

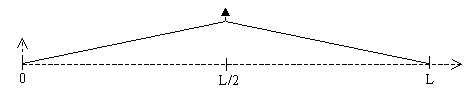
Can you figure out which of the modes shown in Demonstration 4a could be combined to create this shape?

Click here for an animated-audio presentation that will help you answer this question.

You should be able to see from the animation that while the modes do combine to create the initial deflection shape shown above, as the string vibrates up and down it does not keep such a sharp bend at the center. This is because these modes (shape patterns) are all vibrating at different frequencies. You may also notice in the animation that it seems like 2 pulses are traveling away from the excitation point (plucked point), and then getting reflected at the string ends. This is another way to look at it, as waves that are traveling back and forth along the string.

The combination of modeshapes needed to create a particular initial deflection shape can be calculated using Fourier Series. Jean-Baptiste Joseph Fourier (1768 - 1830), French physicist and mathematician, first utilized Fourier Series to develop a theory for the conduction of heat. Click here (Under construction.) to review the basic application of Fourier Series (High school level math).

Actually, the guitar string is plucked near one end, near the bridge. An approximate location might be at x = L/5 as shown in the diagram.

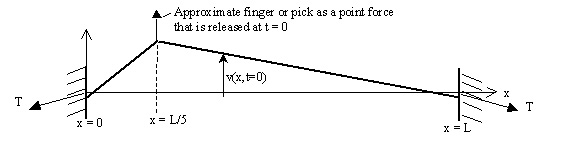
Click here to see an Audio - Visual Demonstration of the response of a Guitar String Plucked at its x = L/5.

Other Guitar Factors
Of course, the tones you have heard do not sound exactly like that of a guitar. There is a lot more that goes into the sound a guitar makes than just the vibrating string. In fact, one of the end conditions, the bridge, is really not a fixed condition on the string. It is through vibration of the bridge caused by the strings that vibratory energy in the strings is transmitted to the guitar body and its air chamber. But, the bridge vibration amplitude is fairly small relative to that of the string and the fixed end condition is a good approximation for the string. Even though the guitar body and its air chamber vibrate with less amplitude than the string they much more effectively couple to the surrounding air to produce the guitar sound. For an electric guitar (not acoustical electric) there are electromagnetic transducers (known as pickups) located at discrete locations along and near the string. They produce a voltage signal proportional to the motion of the string at those discrete locations. Some of the other vibrational factors creating the acoustical guitar sound are the subject of the following lesson.

Bowed Strings
The vibratory motion of a bowed string is quite different than that of a plucked string. As the bow is drawn across the string of a violin, the string appears to vibrate back and forth smoothly between two curved boundaries, like a free string vibrating in its fundamental mode. But this appearance of simplicity is deceiving. If we took a high-speed photograph of the bowed violin string, we would find that the string is nearly straight with a sharp bend at one point; at certain times it resembles the initial shapes of the plucked strings shown in the demonstrations above. If we slow down the motion, we'll also see that during the greater part of each vibration, the string is carried along by the bow. Then it suddenly detaches itself and moves rapidly back until it is caught by the moving bow again.See animation.

Why does the violin string alternate between getting stuck to the moving bow and then sliding along in the opposite direction of its motion. This has to do with the fact that the force of friction between the two objects, bow and string, is less when they are sliding past each other than when they are moving together. As the bow pulls the string away from its straight position, the tension in the string will want to restore it to rest. As the string moves further away from its rest position this restoring force will eventually overcome the friction between the string and bow and the string will start to move. As it starts to move the friction force between it and the bow decreases more and more and the string continues to pick up speed. Finally it goes through the rest position and now the force from the string tension is acting in the same direction as the bowing direction. Eventually, the string slows down and gets stuck again to the bow. It is pulled back through the rest position and the whole process repeats itself.

It is important to note that the beginning and the end of the slipping are triggered by the arrival of the bend (slipping begins when the bend arrives from the nut and ends when it arrives again from the bridge). This time period is set by the same three parameters as before, tension T, mass per unit length µ and string length L. If friction alone determined the beginning and the end of slipping, the vibrations would be irregular rather than regular.

This type of "stick and slip" motion seen between the bow and string is a very common cause of many of the vibrations we see or hear around us everyday. Examples less pleasant sounding include brake squeel, chalk screeching on a blackboard and tool chatter in machining operations.

Another pleasant sounding musical instrument, very popular in the 19th century, that uses this principle is the glass harp. A glass harp consists of a number of drinking glasses filled with different levels of water. One wets their fingers and the rims of the glasses and then runs their finger along the rims causing the glass to vibrate at its resonant frequencies. By filling the glasses with different amounts of water, one can control (or tune) the resonant frequencies to the desired tones.

The limits on the bowing conditions are the limits on the conditions at which the bend can trigger the beginning and the end of slippage between bow and string. For each position of the bow, there is a maximum and minimum bowing force, as shown here. The closer to the bridge the instrument is bowed, the less leeway the violinist has between minimum and maxi um bowing force. Bowing close to the bridge (sul ponticello) gives a loud, bright tone, but requires considerable owing force and the steady hand of an experienced player. Bowing further from the bridge (sul tasto) produces a gentle tone with less brilliance.

The sound radiated from the violin depends more on the side ways force applied to the bridge (which in turn transmits this force to the top plate) than on motion of the string, itself. The force applied to the bridge is in the direction of the string. The following animation shows how this force varies as the string vibrates. See animation.

In the ideal case of a completely flexible string vibrating between two fixed end supports, this force has a sawtooth waveform with a spectrum of harmonics varying in amplitude as 1/n. This can be determined using Fourier series - See derivation. (Under construction) In actual practice, the wave form of the force is modified by the string stiffness, mechanical properties of the bridge, and other factors.

The motion of the top plate, which is the source of most of the violin sound is the result of a complex interaction between the driving force from the bridge and the various resonances of the violin body. It is not simply proportional to the force applied to the bridge. The violin body will be considered in the next lesson.

For further discussion of the bowed string instrument follow this link

Experimental Study of Bowing near and far from the bridge on a Cello
- Abby Stoica, 7th Grade student, Link (under construction).

Changing pitch on a single string
Remember, the natural frequencies of vibration of the string on determined by three things: µ, T and L. The length L can be easily shortened with one's finger on the neck of the instrument. Some string instruments, like guitars have bars called frets on their neck at the certain distances. By pressing the string behind the fret bar, the effective end of the string is shifted to the fret location. For other instruments, like the violin, it is the player's finger, itself, pressed on the string that determines it new end location.

Spacing the frets on a guitar, for example, presents some interesting design problems. The frequency ratio of semitone intervals on the scale of equal temperament is 1.05946. So, to increase by one semitone, what fraction of the current distance L of the string should it be decreased?
Answer.

Another problem in guitar design is the fact that pressing down a string against a fret increases the tension T slightly. This will raise the fundamental frequency f1 more than intended. To compensate for this, the actual distance from the nut to the saddle is made slightly greater than the scale length used to determine the fret spaceings. This small extra length is called the string compensation, and it usually ranges from between 1 - 5 mm on acoustic guitars to several centimeters on an electric bass. Bass strings require more compensation than treble strings, and steel strings require considerably more than nylon strings. A guitar with high action (larger clearance between string and frets) requires more compensation than one with a lower action.

Playing "harmonics" to tune an instrument
Guitarists often tune their instrument by using "harmonics". This refers to lightly resting a finger on the string at certain locations and plucking the string with a different finger or pick. The string's length L is not changed by the finger. But, the finger will dampen all of the modes of vibration of that string except those modes that do not have significant motion at the finger position (they are node points for that mode). For example, placing the finger at 1/3 L down the neck will dampen all modes of vibration except those associated with the following harmonics of the fundamental: 3, 6, 9, etc. The third harmonic will be dominant. Note, this is not the same note that would be played if the string was fixed by the finger at 1/3 L. Then the new length would be 2/3 L corresponding to a perfect fifth.

Other factors
There are numerous other factors related just to the string, itself, of the string instruments. The attack and decay of the plucked or bowed string gives added time-dependent features to the timbre. There are at least 8 different ways to bow the string.

Even with these considerations, just studying the string does not give the whole picture. The rest of the instrument, the primary path to the ear, will significantly affect things. We will learn about this in the next lessons.

Acoustics & Vib. Lab.