| | | Index of Lessons | | | Next Lesson | | | Home | | | Acoustics & Vib. Lab. | | | |
- Lesson 1 -
What's in a single musical tone
In Music Theory one learns that a single note has 4 properties:
pitch, timbre,
loudness
and duration. These are subjective but they are closely linked to specific
physical parameters. Let's take a closer look at what each of these qualities mean.
(Go to summary.)
Pitch
Pitch is that characteristic of sound that makes it sound high or low or that determines its
position on the musical scale. Pitch is related to the repetition rate of
the waveform of a sound. For a
pure tone
, this corresponds to the
frequency; for a
complex tone
it usually (but not always) corresponds to the
fundamental frequency.
Frequency is the
most important contributor to the sensation of pitch. Other lesser contributors to pitch
include intensity,
spectrum,
duration, amplitude envelope,
and the presence of other sounds.
 |
A demonstration of pitch using pure and complex tones. |  |
Create and compare your own pure and complex tunes
| |
Here you can pick a frequency - crossmatched to the note, and select the harmonics to include and their relative amplitude compared to the fundamental. | |
| |
Click here to hear some examples regarding Pitch and Circularity. | |
Timbre
The American National Standards Institute (ANSI) defines timber as "... that attribute of auditory sensation in terms of which
a listener can judge that two sounds similarly presented and having the same loudness (intensity)
and pitch are
dissimilar". Timbre is a catch-all for all sound properties that do not directly influence pitch, loudness or duration.
Primary properties that affect the timbre of a sound are the: (1) spectrum, (2) tonal envelope, (3) rate and depth of amplitude or frequency modulation (vibrato) , and (4) degree of inharmonicity of partials . Subjectively, the sensation of timbre is often characterized by the verbal ranges dull-sharp, compact-scattered colorful-colorless.
| (1) | Effect of Spectrum on Timbre.
The effect of spectrum on timbre can be heard if we focus on the middle, steady portion of a note played on an instrument. |
| |
Click here for a demonstration of effect of spectrum on timbre | |
| |
Click her for additional audio-visual demonstrations of the effect of spectrum on timbre | |
| |
For MERIT Program participants - access your musical sounds recorded in class | |
| (2) | Effect of Temporal Envelope on Timbre.
The spectrum of a tone alone does not distinguish its timbre. When a note is played on virtually any musical instrument, there is an initial transient "attack" period followed by steady-state and decay portions. Select an instrument and a note from the table below. Now the "attack" portion of the tone will be heard as well as the steady-state portion. A visual representation of the sound as a function of frequency (its spectrum) and as a function of time will be generated. This is known as a spectrogram. |
| |
Click here for a demonstration of Temporal Envelope on Timbre | |
| |
Click her for additional audio demonstrations of the effect of envelope on timbre | |
| (3) | Rate and depth of amplitude or frequency modulation: Vibrato.
The American National Standards Institute (ANSI) defines vibrato as: " ... the family of tonal effects in music that depend on periodic variations of one or more characteristics in the sound wave."When the particular characteristics are known, the term 'vibrato' should be modified accordingly: e.g., frequency vibrato, amplitude vibrato, phase vibrato, and so forth. Frequency vibrato may also be referred to as frequency modulation (FM) and amplitude vibrato may also be referred to as amplitude modulation (AM). With musical instruments or the human voice, it is almost impossible to have FM without AM because of the effect of the room and because they are often coupled in the instrument. AM can occur without FM, but it is uncommon. The modulation rate varies with individual performers, an average rate for both singers and instrumentalists being around 7 Hz. Singers seem to use a slightly greater depth of frequency vibrato than instrumentalists do, however. To hear examples and experiment with vibrato click here. |
| |
Click here to hear examples and experiment with vibrato. | |
| (4) | Inharmonicity of partials.
When a note is played on most instruments, the instrument emits a complex tone that often contains the fundamental frequency and a number of frequencies that are almost integer multiples of the fundamental, but not quite. The human ear, nonetheless, formulates the pitch from these "near harmonics" or "near integer multiples". For example, the pitch of bells and chimes is determined primarily by three frequencies that are almost but not exactly in the ratio of 2 : 3 : 4. The fact that they are not quite exactly in a perfect integer ratio does modify the timbre. |
| | | | | | | | | | |
Loudness
In a sound wave there are extremely small periodic variations in atmospheric pressure to which our ears respond in a
rather complex manner. The minimum pressure fluctuation to which the ear can respond is less than one billionth (10-9) of
atmospheric pressure. This corresponds to a sound pressure amplitude of 2 x 10-5 N/m2. The threshold of pain corresponds
to a pressure amplitude approximately one million (106) times greater, but still less than 1/1000 of atmospheric pressure.
Because of the wide range of pressure stimuli, it is convenient to measure sound pressures on a logarithmic scale, called the decibel (dB) scale. Although a decibel scale is actually a means for comparing two sounds, we can define a decibel scale of sound level by comparing sounds with a reference sound having a pressure amplitude p0 = 2x10-5 N/m2 assigned a sound pressure level of 0 dB. Thus we define sound pressure level as:
Lp = 20 log p/p0.
Expressed in other units, p0 = 20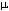 
Pa = 2x10-4 dynes/cm2 = 2 10-4
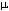bars.
(For comparison, atmospheric pressure is
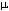105 N/m2, or 106 bars). Sound pressure levels are measured by a sound level meter, consisting of a
microphone, an amplifier, and a meter that reads in decibels.
In addition to the sound pressure level, there are other levels expressed in decibels, so one must be careful when reading technical articles about sound or regulations on environmental noise. One such level is the sound power level, which identifies the total sound power emitted by a source in all directions. Sound power, like electrical power, is measured in watts (one watt equals one joule of energy per second). In the case of sound, the amount of power is very small, so the reference selected for comparison is the picowatt (10-12 watt). The sound power level (in decibels) is defined as
Lw = 10 log W/W0,
where W is the sound power emitted by the source, and the reference power W0 = 10-12 watt.
Another quality described by a decibel level is the sound intensity, which is the rate of energy flow across a unit area. The reference for measuring sound intensity level is I0 = 10-12 watt/m2, and the sound intensity level is defined as
LI = 10 log I/I0.
For a free progressive wave in air (e.g., a plane wave traveling down a tube or a spherical wave traveling outward from a source), sound pressure level and sound intensity level are nearly equal (Lp = LI). This is not true in general, however, because sound waves from many directions contribute to sound pressure at a point.
The relationship between sound pressure level and sound power lever depends on several factors, including the geometry of the source and the room. If the sound power level of a source is increased by 10 dB, the sound pressure level also increases by 10 dB, provided everything else remains the same. If a source radiates sound equally in all directions and there are no reflecting surfaces nearby (a free field), the sound pressure level decreases by 6 dB each time the distance from the source doubles.
Loudness is a subjective quality. While loudness depends very much on the sound pressure level, it also depends upon such things as the frequency, the spectrum, the duration, and the amplitude envelope of the sound, plus the environmental conditions under which it is heard and the auditory condition of the listener.
Loudness is frequently expressed in sones. One sone is equal to the loudness of a 1000-Hz tone at a 40-dB sound pressure level, and two sones describes a sound that is judged as loud, etc.
The range of sound level in musical performance, known as the dynamic range, may vary from a few decibels to 40 decibels (dB) or more, depending on the music (loud peaks and pauses may cause the instantaneous level to exceed this range). Click here to see a graph of the approximate range of sound level and frequency heard by the music listener.
Composers use dynamic symbols to indicate the appropriate loudness to the performer. Different instruments have different dynamic ranges, however, so fortissimo vs. pianissimo will yield different results. Click here to see a table of the 6 standard levels and typical instrument dynamic ranges.
Duration
This one is pretty self-explanatory. Duration refers to the time length of a tone. It is especially
important for musicians because it is concerned with rhythm - one of the basic elements of music.
Summary
A single tone is defined by 4 subjective qualities, pitch, timbre,
loudness
and duration. These are more or
less related to certain quantifiable physical parameters. Click here to see a
table that qualitatively denotes those relationships.
| | | Index of Lessons | | | Next Lesson | | | Home | | | Acoustics & Vib. Lab. | | | |